1. 介绍

1.1 背景

1.1.1 为什么基于 LFU

数据访问模式的概率分布不随时间变化时，LFU 产生最高的缓存命中率，但是

  • LFU 需要维护大量的元数据
  • 大多数负载中，访问频率随时间变化

1.1.2 工作

  • 提出 TinyLFU，它是近似 LFU 并高度节省空间。
  • 提出了 W-TinyLFU，它是基于 TinyLFU 的一个优化，能更好地处理突发工作负载
  • 对 上述两种 LFU 进行了实验
    • TinyLFU 极大提高了驱逐性能，并且有与原始 LFU 几乎相同的缓存命中率
    • W-TinyLFU 在真实工作负载下，缓存命中率比所有 LFU 变种都高

2. TinyLFU 架构设计

2.1 总览

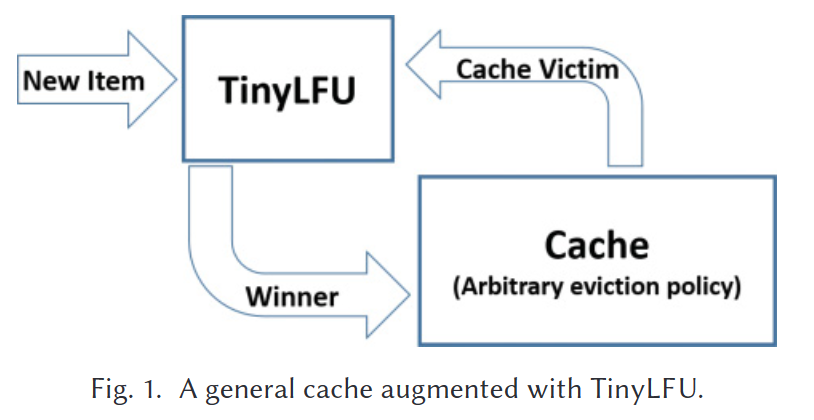
每当有一个 Item 进来

  • 如果 Cache 没有满，直接插入
  • 如果 Cache 满了，会有一个淘汰项 V
  • 比较 Item 和这个 V 的最近频数，胜者插入 Cache 中

总体来说，用了两个技术（近似计数，新鲜度）和两个优化（为了体积更小）。

image.png

2.2 近似计数

TinyLFU 可以选择多种近似计数，只要他们实现下列接口

  • Add(key)：向集合添加一个键
  • Estimate(key)：估计这个键出现了多少次

下面几种 Sketch 算法可以作为 TinyLFU 的近似计数

  • CBF：一个 key 哈希 k 次，对应 k 个 Counter，最小的为 Estimate。
  • Minimal Increment CBF
  • CM-Sketch

2.2.1 Count Min Sketch

CM-Sketch 的内部数据结构是一个二维数组$count[h][w]$，每一行都有一个哈希函数$h_r$，它们两两独立。

  • Add(x, c)：更新时，算出$d$个不同哈希值，把对应的行加上$c$
  • Estimate(x)：算出$d$个不同哈希值，所有对应行计数的最小值

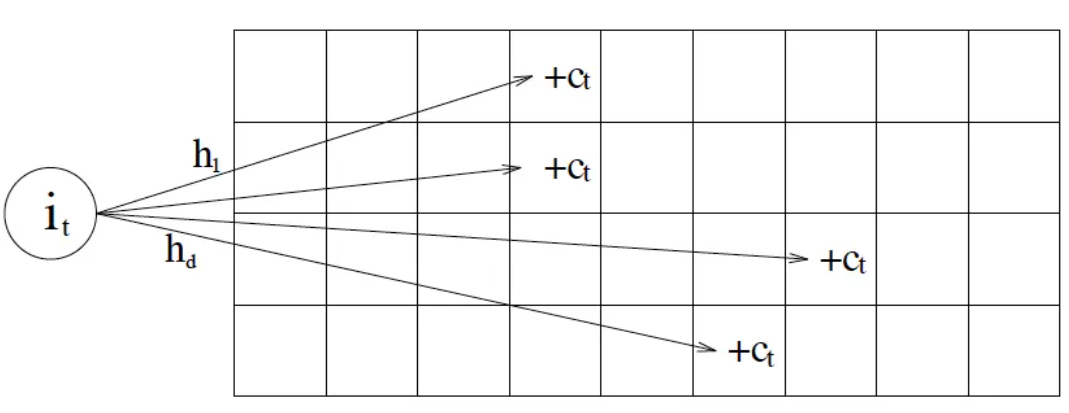
image.png

误差保证： $h=\lceil ln(1/\delta)\rceil$,$w=\lceil e/\varepsilon \rceil$下，保证总误差小于$\varepsilon$的概率为$1-\delta$。

2.3 保鲜机制

提出一种基于计数器的新鲜度保持方法，有一个全局计数器 S 和 样本大小 W

  • 当我们在 Sketch 添加一个项目，S = S + 1
  • 如果 S == W，定义一个保险（Reset）操作
    • 让 Sketch 中所有计数除以 2
    • S = S / 2

2.4 空间优化

2.4.1 减少 Counter 的大小

在新鲜度机制下，原有 Sketch 的 Counter 值域最大为 W，因此 Counter 需要 log(W) 位。

实际值域真的需要那么大么？我们假设 Cache 的大小为 C，所有访问频率占比高于 1/C 的都属于这个 Cache，所以频数高于 W/C 就说明一定在 Cache 中，因此Counter 用 W/C 的值域就能够表达数据是否常用且新鲜。

2.4.2 Doorkeeper 门卫机制

在很多工作负载下，访问频数很少的数据占很大比例（所谓八二定律），所以把访问频次为一的数据项拦截住可以节省系统的开销。为此，TinyLFU 采用 Doorkeeper 机制，在近似计数器前放一个 Bloom Filter 作为门卫。相当于 Counter 为 1 bit 的 CBF，从而一定程度上降低了近似计数器的空间开销。

image.png

  1. 插入时
  • key 到达后，首先检查它是不是在 Bloom Filiter 中
  • 如果它在 Bloom Filiter 中，就插入到近似计数器中
  • 如果不在，就插入到 Bloom Filiter 中
  1. 查询时
  • 如果它在 Bloom Filiter 中，就把近似计数器中的值加1，并返回估计值
  • 否则，只返回近似计数器的估计值，不加1
  1. 保险时
  • 近似计数器所有值减半，全局计数器减半
  • 清除 Bloom Filiter

3. W-TinyLFU：改进 TinyLFU

3.1 TinyLFU 的问题

  • 在 Zipf 分布的数据上表现不及预期
  • 从理论上看，TinyLFU 相比 LRU 的竞争比率更差
  • 我们希望过去一段时间的 Item 一定在 Cache 中，而 TinyLFU 不能保证这一点

3.2 W-TinyLFU 架构

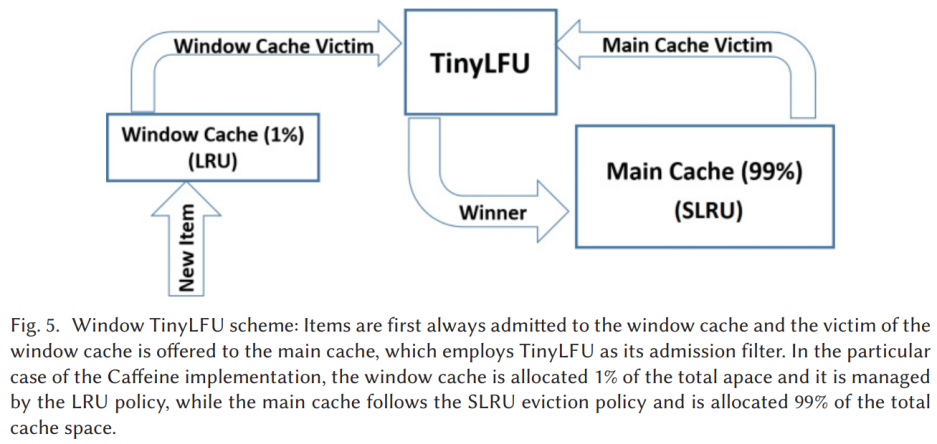
image.png

和 TinyLFU 不同，W-TinyLFU 由一个窗口缓存（Window Cache）和主缓存（Main Cache）组成。窗口缓存的目的是：保留最近一段时间使用过的项。

理论上主缓存可以选择任何 Cache 和任何类型的逐出策略。在 Caffeine 中，作者选择了 SLRU（Segmented LRU），它分为两个段：淘汰段（Probation Cache）和保护段（Protected Cache）。

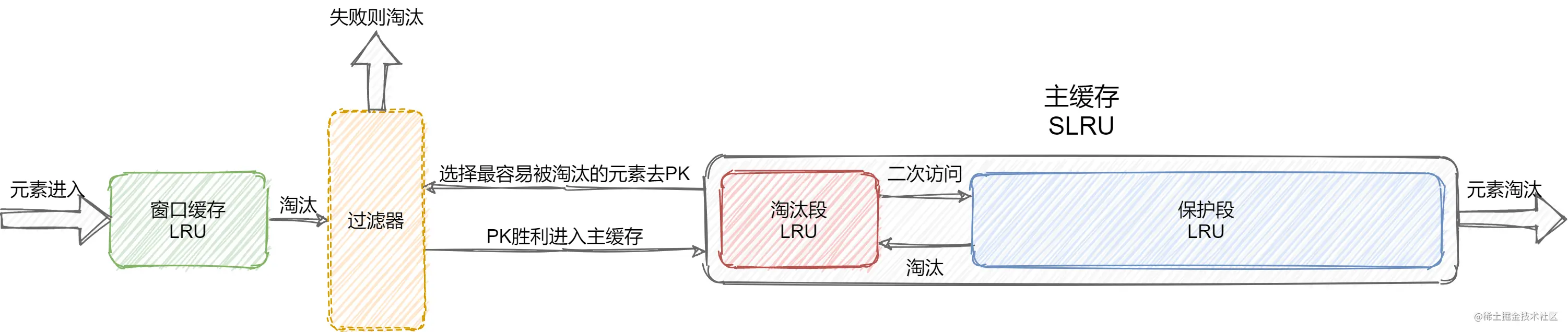
image.png

3.2.1 首次淘汰

当数据项插入缓存时，总是先插入窗口缓存中

  • 如果窗口缓存未满，不会有元素被淘汰，插入结束
  • 如果窗口缓存满了，就会淘汰一个数据项 Item，这个数据项将会插入主缓存中
    • 数据会先插入主缓存的淘汰段
      • 淘汰段 没有满，直接插入 Item，插入结束
      • 淘汰段满了，先淘汰一个数据项 V
      • TinyLFU 比较一下 Item 和 V 的最近频次，胜者插入淘汰段，流程结束

3.2.2 二次淘汰

淘汰段缓存项的访问频数到达一定阈值后，会晋升到保护段中，如果此时保护段满了，它就会二次淘汰一个数据项，把他放入淘汰段。假设写入淘汰段的数据项为 Item。

  • 淘汰段 没有满，直接插入 Item，流程结束
  • 淘汰段满了，先淘汰一项 V
  • TinyLFU 比较一下 Item 和 V 的最近频次，胜者插入淘汰段，流程结束

3.2.3 淘汰规则

当数据项 Item 和 一个淘汰项 V 准备写入缓存 C 时，比赛的规则如下。假设 C(x) 为 x 的访问频率

  • C(Item) > C(V)，Item 获胜
  • C(Item) <= C(V)，分两种情况
    • C(Item) < 5，V 获胜
    • 否则，在 Item 和 V 中随机选择一个获胜

胜者可以写入缓存 C，败者将被淘汰。

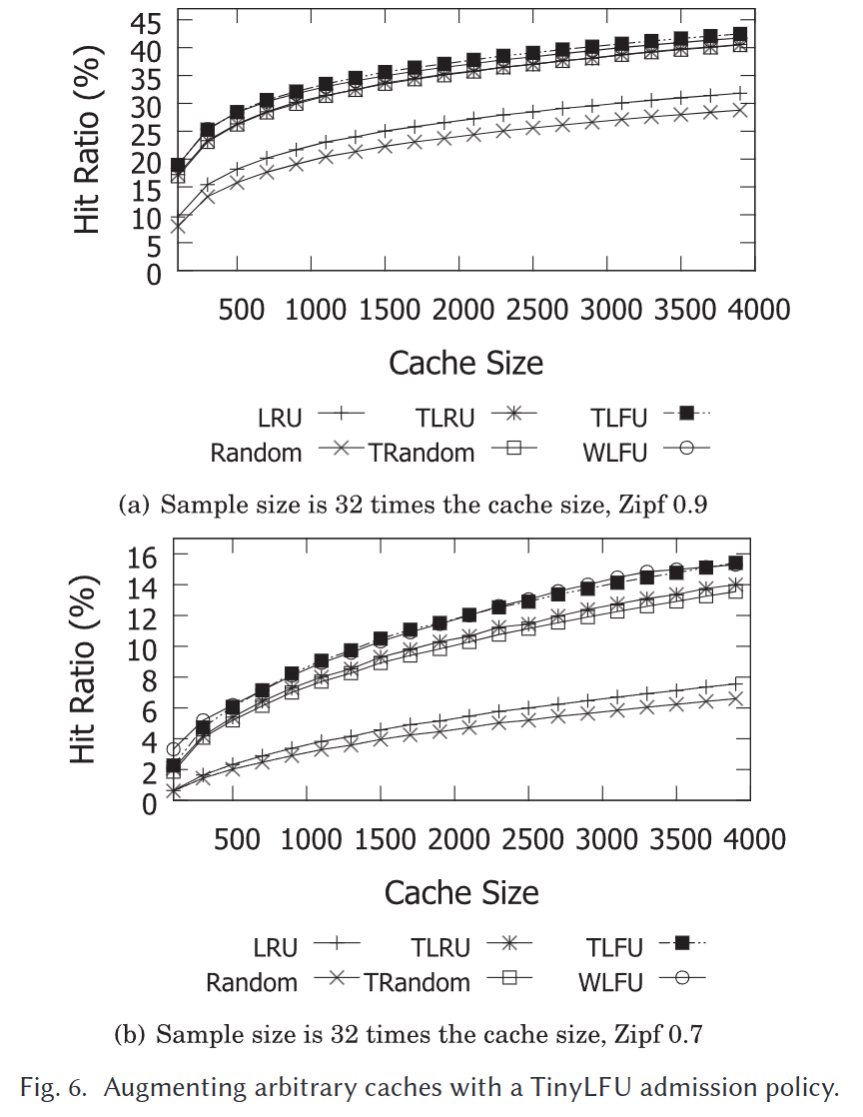
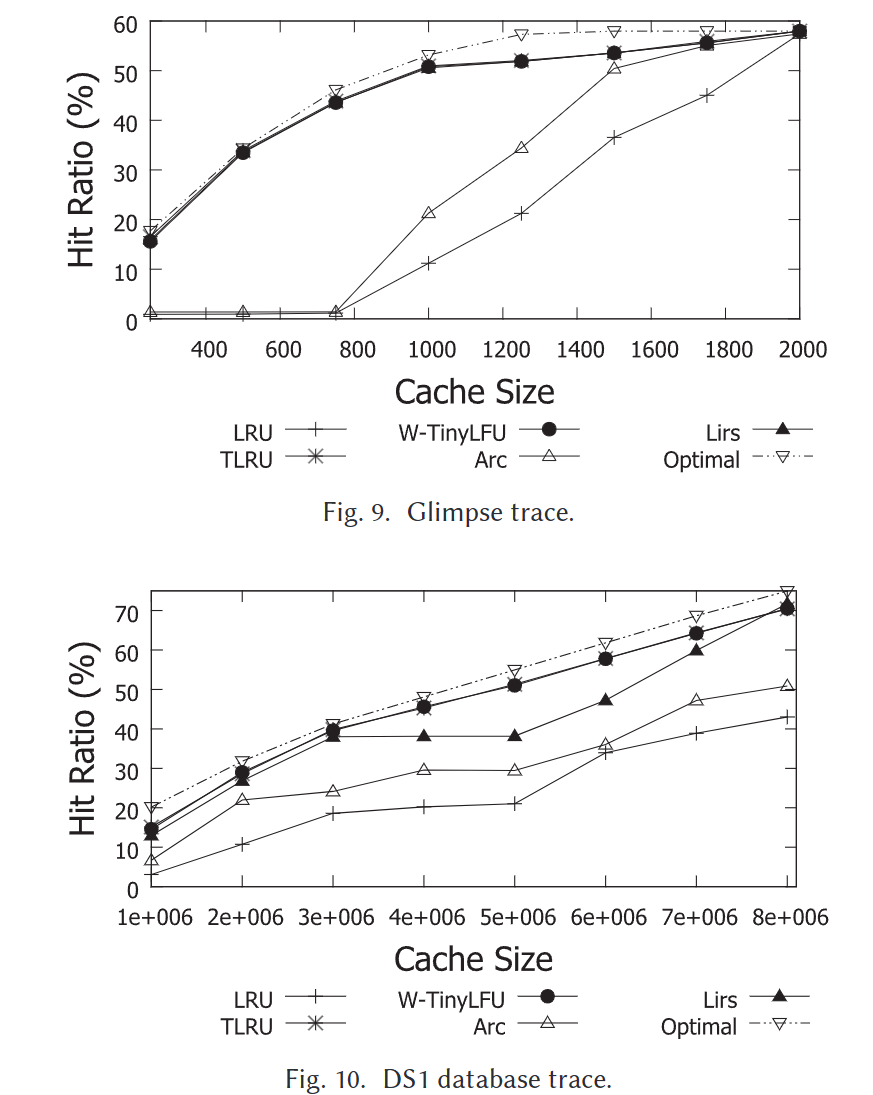
4. 实验

在众多缓存替代策略中 SOTA。

image.png

image.png

5. 参考文档